
Archytas of Tarentum, who was born around the year 435 BC in what is now Taranto, Apulia, Italy, was another in a long line of brilliant polymaths from Ancient Greece, a noted military general and strategist who also made his mark in the realms of geometry, physics, astronomy, and music.
A friend of Plato, he was a brilliant philosopher, as well. As a scientist, he belonged to the Pythagorean school and became well-known for being the reputed founder of mathematical mechanics.
The son of Mnesagoras, Archytas was taught by Philolaus, and was himself a teacher of mathematics to Eudoxus of Cnidus. They both had Menaechmus as a mathematical student. As a Pythagorean, Archytas purportedly believed that only arithmetic, not geometry, could provide a basis for satisfactory proofs. However, his later invention of what came to be called Archytas’ curve disproved that theory.
As described in the writings of Aulus Gellius—five centuries after he lived—he was reputed to have designed and built the first artificial, self-propelled flying device, a bird-shaped model propelled by a jet of what was probably steam, said to have actually flown some 200 meters.
Known today as the “Pigeon of Archytas,” it is famous for being the basis of many a backyard experiment in the physics of steam. His original apparatus may have been suspended on a wire or pivot for its flight.
Archytas also wrote some lost works on the science of mechanics, as he was included by Vitruvius in the list of the twelve authors of works of mechanics.
Archytas named the harmonic mean, which was important much later in projective geometry and number theory, although he did not invent it. According to Eutocius, Archytas solved the problem of doubling the cube (the so-called Delian problem) with the geometric construction of his eponymous Curve.
Before his time, Hippocrates of Chios had reduced this problem to finding mean proportionals. Archytas’ theory of proportions is treated in book VIII of Euclid’s “Elements,” where the construction for two proportional means is equivalent to the extraction of the cube root.
According to Diogenes Laërtius, this demonstration, which uses lines generated by moving figures to construct the two proportionals between magnitudes, was the first in which geometry was studied with concepts of mechanics. The graceful Archytas curve, which he used in his solution of the doubling the cube problem, is named after him.
Pericles, a brilliant strategist of his time in Magna Graecia
Politically and militarily, Archytas appears to have been the dominant figure in Tarentum, in what was then Greater Greece in his generation, somewhat comparable to Pericles in Athens a half-century earlier.
The Tarentines elected him strategos, or “General,” seven years in a row—a move which required them to violate their own rule against successive appointments. He was allegedly undefeated as a general in Taranto’s campaigns against its southern Italian neighbors.
The Seventh Letter of Plato states that Archytas attempted to rescue Plato during his difficulties with Dionysius II of Syracuse.
In his public career, Archytas had a reputation for virtue as well as efficacy.
Some scholars have argued that the polymath, Archytas, may have served as a model for Plato’s “philosopher king,” and that he influenced Plato’s political philosophy as shown in The Republic and other works, especially as is obvious in his question “how does a society obtain good rulers like Archytas, instead of bad ones like Dionysius II?”
The crater called “Archytas” on the Moon was named in his honor by NASA.
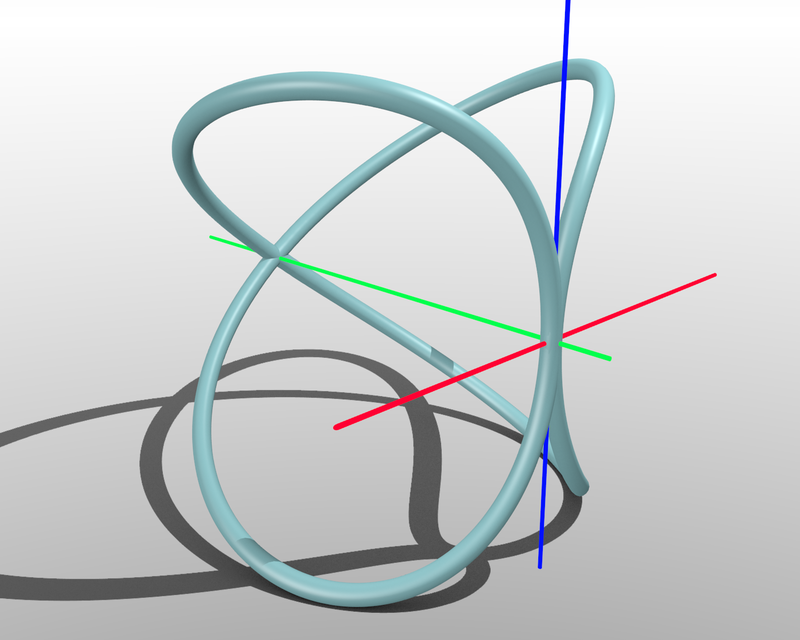
Archytas’ eponymous curve
The Archytas curve is created by placing a semicircle (with a diameter of d) on the diameter of one of the two circles of a cylinder (which also has a diameter of d) such that the plane of the semicircle is at right angles to the plane of the circle and then rotating the semicircle about one of its ends in the plane of the cylinder’s diameter. This rotation will cut out a portion of the cylinder forming the Archytas curve.
Another way to think about this shape is that the Archytas curve is basically the result of cutting out a torus (a surface or solid) formed by rotating a hemisphere of diameter d out of a cylinder also of diameter d. A cone can go through the same procedures and also produce the Archytas curve. Archytas used his curve to determine the construction of a cube with a volume of one third of that of a given cube.
Although a friend of Plato, after his invention of the curve, he was criticized for “contaminating” the purity of geometry with mechanics.
Plutarch says in his Symposiacs, Book VIII, Question 2: “And therefore Plato himself dislikes Eudoxus, Archytas, and Menaechmus for endeavoring to bring down the doubling the cube to mechanical operations; for by this means all that was good in geometry would be lost and corrupted, it falling back again to sensible things, and not rising upward and considering immaterial and immortal images, in which God being versed is always God.”
In music, Archytas’ greatest contribution was the creation of ratios that present an interrelated intervallic system. Archytas’ ratios were providentially preserved by Ptolemy.
Since much of ancient Greek musical theory is lost, this system, which was recorded in Plato’s Republic, offers valuable evidence about pre-Aristoxenian Greek music, especially about “harmonia” and the technique of transposition, which later were developed into complete systems of octave species and “tonoi,” to use the Greek terms.
See all the latest news from Greece and the world at Greekreporter.com. Contact our newsroom to report an update or send your story, photos and videos. Follow GR on Google News and subscribe here to our daily email!



